The study of electric charge and electric flux along with the surface is the Gauss law. It is one of the basic laws of electromagnetism, which is applicable for any type of closed surface known as a Gaussian surface. This law is explained and published by a German mathematician and physical Karl Friedrich Gauss law in the year 1867. It describes the relation between the intensity of the electric field of a surface and the total electric charge enclosed by that surface. This article gives an overview of gauss law in dielectrics and magnetostatics with a mathematical expression.
What is Gauss Law?
Gauss law is one of Maxwell’s equations of electromagnetism and it defines that the total electric flux in a closed surface is equal to change enclosed divided by permittivity. According to this law, the total flux linked with a closed surface is 1/E0 times the change enclosed by a closed surface. The electric flux in an area means the product of the electric field and the area of the surface projected in a plane and perpendicular to the field.
Gauss Law Formula
As per this law, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface.
Consider if, Φ is the total flux and E0 is the electric constant, then the Total electric charge Q enclosed by closed surface can be expressed as follows
Q= ΦE0
Therefore, the gauss law formula can be expressed as below
ΦE= Q/E0
Where, Q= Total charge within the given surface, E0 is the electric constant.
This concept is simple and it can be understood very easily by considering the gauss law diagram shown in the figure below. The total electric flux through the closed surface depends on the charges of the enclosed surface and the charges on the outside of the surface don’t contain any flux. The shape of the surface is considered arbitrarily. Since the total electric flux is independent of the location of charges inside the closed surface. This imaginary surface is called a gaussian surface, which depends on the configuration of charges and the type of symmetry that exists in the charge configuration. Mostly cylindrical and planar surfaces are chosen
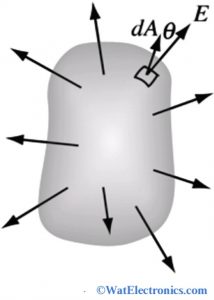
Gauss Law Diagram
Gauss Law SI Unit
The Gauss law SI unit is given below.
If the electric field is constant, the electric flux passing through the surface of vector area S is
ΦE = E .S = E S Cos ө
If an electric field is not constant, the electric flux through small surface area dS is given by
d ΦE = E. dS
Where E = Electric field
dS = differential area on closed surface
Electric flux has SI units of voltmeters (V m)
An electric field is a region of space around a charged particle or between two voltages; it exerts a force on charged objects in its vicinity.
Gauss Law Mathematical Expression
According to Gauss law, the total flux in a closed surface area is 1/E0 times the charge confined by a closed surface.
∮E. ds = (1/ E0) q
For an instance, a point charge q is positioned in a cube edge. Then as per gauss law, the flux generated through each face of a cube is q/6 E0
As per this law, the total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface.
Consider if, Φ is the total flux and E0 is the electric constant, then the Total electric charge Q enclosed by closed surface can be expressed as follows
Q= Φ E0
Therefore, the gauss law formula can be expressed as below
ΦE= Q/E0
Where, Q= Total charge within the given surface, E0 is the electric constant
Derivation
The gauss law derivation is given below.
Deriving gauss law using coulombs law,
CASE 1: Spherical surface enclosing single point charge
Let suppose we have a single stationary point charge with a magnitude of E
E= q/4ΠE0r2
ΦE = ∮E. dA
= ∮ q/4ΠE0r2. dA
= q/4ΠE0r2§ dA
= qA/4ΠE0r2
= q4Πr2/4ΠE0r2
= q/E0
ΦE = ∮ E. dA = q/E0
CASE 2: Irregular surface enclosing the same point charge
Let the same type of field lines pass through the surface A1 and A2
ΦE = ∮A1 E. dA = ∮A2 E. dA = q/E0
∮ E. dA = q/E0
Gauss Law in Dielectrics
Consider a parallel plate capacitor with equal area A and charge density σ and there will be a vacuum between the plates. The following diagram explains this law in dielectrics between the two parallel plates.
Then we can evaluate field vector E0 in the region between the plates using the gauss law.
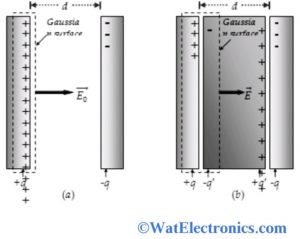
Gauss Law in Dielectrics
Let us consider a Gaussian surface with cuboids shape and one face is Gaussian the flux will not pass through it, and then the flux will not pass through the perpendicular face to this face. Therefore the flux will only pass through the face which is parallel to the positive plate.
Consider E0 constant of Gaussian surface and ө is the angle between field vector and area vector
∯S E0. dα = q/E0
∯S E0 dα cosө = q/E0
∯S E0 dα = q/E0
E0∯S dα = q/E0
E0A = q/E0
E0 = q/E0A
Here q= A σ
E0 = A σ /E0A
E0= σ/ E0
Gauss Law for Magnetostatics
This law for magnetism applies to the magnetic flux through a closed surface. In this case, the area vector points out from the surface.
Since magnetic field lines are continuous loops, all closed surfaces have as many magnetic field lines going in as coming out. Hence, the net magnetic flux through the closed surface is zero.
Net flux = ʃ B. dA = 0
Therefore the net sum of all currents in the enclosed surface is Null. Gauss law for charges was a very useful method for calculating electric fields in highly symmetric situations. Gauss law for magnetostatics is used very rarely.
Significance
This section will let you a clear explanation regarding the significance of Gauss law. Gauss’s law statement is correct and suitable for any closed surface independent of the size or shape of the particular object.
The term Q in the formula of gauss law indicates the summation of all charges which are completely enclosed in the object irrespective of the position of the charge on the surface.
In some of the selected surfaces, there exist both internal and external charges of an electric field. The selected surface for the functionality of gauss law is termed as Gaussian surface, but this surface should not be passed through any kind of isolated charges.
This is mainly employed for the simplified analysis of the electrostatic field in the scenario that the system holds some equilibrium. This will only happen when we choose an exact Gaussian surface.
Examples
1). An enclosed Gaussian surface in the 3D space where the electrical flux is measured. Provided the Gaussian surface is spherical which is enclosed with 40 electrons and has a radius of 0.6 meters.
- Calculate the electric flux that passes through the surface
- Find the electrical flux having a distance of 0.6 meters to the field measured from the center of the surface.
- Know the relation that exists between the enclosed charge and the electric flux.
Answer
With the formula of electric flux, the net charge that is enclosed in the surface can be calculated. This can be achieved by charge multiplication for the electron with the entire electrons that appear on the surface. Using this, the free space permittivity and the electric flux can be known.
Ф = Q/є0 = [40(1.60 * 10-19)/8.85 * 10-12]
= 7.42 * 10-12 Newton*meter/Coulomb
Answer
Rearranging the equation of electric flux and expressing the area as per radius can be used to calculate the electric field.
Ф = EA = 7.42 * 10-12 Newton*meter/Coulomb
E = (7.42 * 10–)/A
= (7.42 * 10–)/4∏(0.6)2
As the electric flux has a direct proportion with the enclosed electric charge, this signifies that when the electric charge on the surface enhances, then the flux which passes through it also will be enhanced.
Advantages
The advantages of gauss law are as follows
When compared to coulombs law, it provides specific force direction with proper accuracy with its proper general cases.
Gauss theorem is more efficient in all closed objects and surfaces for purpose of finding an electric field and also it will work effectively in the distribution process when compared with coulombs law.
Disadvantages
The disadvantages of gauss law are as follows
The limitation of the gauss law is that it will only calculate the electric field in some special cases. We cannot use gauss law in the calculation of the field due to electric dipole.
Applications
Following are the important applications of Gauss law
- This is most useful to solve complex electrostatic problems involving unique symmetries such as cylindrical, spherical, or planar symmetry.
- This can be very useful to calculate field intensity due to infinitely long uniformly charged wire.
- If the charge distribution lacks symmetry of application, in those cases we can use this law to calculate point charge fields of the individual charge elements which are present in the object
- This law can be used to simplify the evaluation of the electric field simply and easily.
- In some of the complex situations, where the calculation of the electric field is complex, then this law is used in integral form.
Know more about DeMorgan’s Theorem.
Please refer to this link to know more about Biot Savarts Law MCQs.
Please refer to this link to know more about Gauss Law MCQs.
Thus, this is all about an overview of Gauss law – definition, formula, SI unit, mathematical expression, derivation, diagram, in dielectrics, in magnetostatics, significance, examples with solutions, advantages, disadvantages, and its applications. Here are a few questions for you : What are Maxwell’s equations of electromagnetism? What is Snell’s Law?