Initially, Ptolemy a scientist from Alexandria discovered the relation that exists between refraction angles, but his invention failed for a minimal range of angles. In the scope of this Alhazen invented the law of refraction and finally, it was named Snell by the Persian researcher Ibn Sahl. After this many inventors worked upon this law to know the exact principle of this law. Finally, with the enhancement of various electromagnetic and optical concepts, Snell’s law was brought into the modern phase. So, this a brief history of how Snell’s law was discovered. Now, this article explains to you clearly of its definition, derivation, equation, and example.
What is Snell’s Law?
This law defines the degree of refraction and states the relation that exists between the angle of refraction, incidence and also describes the refractive law of indices for the provided media like light, glass, and air. As we all know that when light travels from one medium to another, it will undergo either bending or refraction. So, using Snell’s law the angle of bending can be known and it is called Snell’s law of refraction.
To be clear let us understand what refraction is.
When light travels in a vacuum, it has a straight-line path. But, when it moves from one kind of medium to another kind (such as from light to air), there happens refraction. So, refraction basically defined as light bending when traveled across different mediums.
Assume that, when the speed of human and light are compared, then we walk faster when it is ground medium and the walking speed will be lower when we walk in any pool or lake. This happens because water is denser than that of air. So, the same scenario is applied for light. The speed of travel for light is more than compared with the water medium. So, the bending of light takes place and gets refracted. With the above instance, the incident ray that hits the surface and travels across the air. But, upon hitting light is bent and then called a refracted ray. The normal line is in a perpendicular angle to that of the surface. Every medium has its refractive indexes.
- When the medium is air, then the index of refraction is 1.00029
- When the medium is ice, then the index of refraction is 1.31
- When the medium is water, then the index of refraction is 1.33
- When the medium is a vacuum, then the index of refraction is 1.000
- When the medium is acetone, then the index of refraction is 1.36
- When the medium is ethyl alcohol, then the index of refraction is 1.36
So Snell’s law definition is given that “The proportion between sine values of angle of incidence and angle of refraction is a constant value”. This is clearly expressed as
sini/sinr = constant = µ
This is the Snell’s law formula and in the above equation ‘i’ corresponds to an angle of incidence and ‘r’ corresponds to the angle of refraction. And the resultant value is termed as a refractive index. The pictorial representation of the above definition is shown as follows
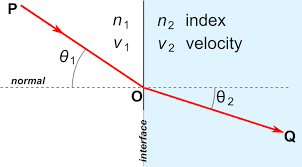
Refraction Of Snells Law
From Fermat’s functional principle, Snell’s law is derived. Fermat’s operating theory defines that light moves in the smallest path and it has less traveling time and given as
n1sinϴ1 = n2sinϴ2
Here, ‘ϴ1’ represents the angle in correspondence to incidence and ‘ϴ2’ represents the angle in correspondence to refraction, and ‘n1’ and ‘n2’ are the mediums.
Snell’s Law Derivation
It can be done from the Fermat’s principle. As per the above equation, there are two mediums and the phase velocities of these are represented as
v1 = c/n1 and v2 = c/n2
Here, ‘c’ represents light speed where the media is vacuum
Let us assume that T is the time taken by the light to travel from M to N
T = [(√x2 + a2)/v1] + [(√b2 + (l-x)2)/v2]
= [(√x2 + a2)/v1] + [(√b2+l2-2lx+x2/v2]
When the above equation is differentiated, it gets minimized to
dT/dx = [x/(v1√x2 + a2)] + [-(l-x)/v2√b2 + (l-x)2] = 0
Here [x/(√x2 + a2)] = sinϴ1 and
[(l-x)/(√b2 + (l-x)2)] = sinϴ2
So, dT/dx = (sinϴ1/v1) – (sinϴ2/v2) = 0
(sinϴ1/v1) = (sinϴ2/v2)
By substituting the phase velocity equation, then
n1sinϴ1/c = n2sinϴ2
n1sinϴ1 = n2sinϴ2 ————This is the final derived Snell’s law equation
Snell’s law can also be derived using Huygen’s principle and from Maxwell’s equation.
Examples
1). When the ray has an angle of refraction as 140 and the refractive index is given as 1.2, then the below derivation explains how to calculate the value of angle of incidence.
Provided that angle of refraction (r) = 200
Refractive index (µ) = 1.2
By using the Snell’s law,
sini/sinr = µ
sini/sin200 = 1.2
sin1 = 1.2×sin200
sini = 1.2×0.342 = 0.41
i = sin 1(0.41) = 20.3
2). When the angle of incidence and angle of refraction is given by 250 and 320, then what is the refractive index?
Provided that angle of refraction (r) = 320
Angle of incidence (i) = 250
By using the Snell’s law,
sini/sinr = µ
sin25/sin32 = µ
0.4226/0.529 = µ
So µ = 0.7975 ~ 0.8
- When a mirage is clearly observed, it is happened by the intense situations of refraction undergone by light and it is termed as total internal reflection.
- When the reflection of either trees or mountains has happened in rivers or lakes, it is the example of Snell’s law
- Extremely implemented in the optical industry
So, these are the few Snell’s law examples
Applications
The applications of snell’s law include the following.
- Snell’s law has extreme applications in various industries mainly in the domain of optical industry. This law is implemented in optical devices like in contact lenses, digital cameras, eyeglasses, kaleidoscope, and in rainbows.
- Through a device called a refractometer, Snell’s law is used to know the refractive index value of liquid medium substances and even employed in candy manufacturing industries.
- The limitation of this law is that it is not implemented to measure the refraction angle of the beam which has a finite beam.
So, this is all about the an overview of Snell’s law which includes formula, its derivation, example problems & its applications. Here, we have gone through the law definition, derivation, formula, examples, and applications. Also few of the other concepts to be known are how the refractive index of Snell’s law varies and Snell’s law datasheet?