Octal Numbering System
The numbering system that consists of ‘8’ digits of numbers in it can be known as Octal Numbering System. This system is almost the same as that of the Hexadecimal system. In this, each number is encoded with three bits grouped. In similar to another system the coding is based on positions. The position allotment starts from the LSB. The weight of each position is the power value of 8. The numbers present in this system are 0, 1,2,3,4,5,6,7.
During the earlier stages of computations in the ‘mini-computers’, this numbering system is preferred. The advantage of this system is that from this format the number can be easily converted into binary.
Octal Numbering System Uses
When the question arises of dealing the large numbers to make the system more efficient for computations this number coding is preferred. Generally, the computer or the processor in it works with binary values. Still, for making it user-friendly this coding is preferred. The length of the coding of this system is one-third of the binary system.
By using the binary digits we can show the encrypted data. But certainly to make the operator understand some coding and decoding is needed. For such purposes, programs can be written in certain languages to convert one numbering format into another.
In sectors like aviation and the computations, these coding systems are preferred. The modernized systems use ’16-bits, 32-bits, 64 bits’ words which are further categorized into 8 bits. In the techniques of encryption, these coding of octal is preferred. This type of encryption is possible with the help of certain devices called encoders.
In practice the Transponders used in Aircraft uses Octal Numbering format for transmitting the code. Further, these codes interrogated with the radar present in the ground. Nowadays because of the new methods of conversion the digital systems prefer the other coding formats.
Binary to Octal Conversion
The difference between the Binary system of numbering and the Octal is that its base representation. The base value of the binary system is 2 whereas the base representation of the octal system is 8. The digits present in binary can be grouped first into three digits. The fact behind this is 2^3=8.
The steps involved in the binary to octal conversion are as follows:
- The most prominent step is to identify the given number is in which format. The representation of a binary number can be understood by its subscript 2.
- The other step involves the grouping of these binary digits from the right side.
- In case while grouping if any group is not filled with three digits. Then 0 bits are added to that group.
- Finally, the number obtained is represented by the subscript of the octal system that is ‘8’.
Examples
Let us discuss the above conversions in detail followed by examples.
- Convert the given code that is in binary 010011 into Octal. The conversion begins with grouping the digits into three. That is
010 011
- After the grouping is completed. Check whether three digits in the group are present or not. If this step is verified then the conversion starts.
- As it is based on positions each group is converted by adding the binary coded numbers. That is 421 for each group.
010 011
421 421
- The binary number where 0 is present. The final number after the code conversion obtained will be zero. If the number is 1 after the conversion it will be the same coded number.
- For 010 the number obtained is 020 and for 011 the number obtained is 021.
- After the coded numbers are obtained it must be added in their respective groups. That is for 010 it is 0+2+0=2. For 011 it is 0+2+1=3.
- Therefore the final obtained number is 23 in octal format.
Further, if the number has any decimal values. Then it is better to prefer the values of the conversion table. Hence by the above method, one form of binary values can be converted into octal. Sometimes the octal language is preferred in the computational systems.
Octal to Binary Table
The purpose of this table is to know for what values of binary the values of octal format are assigned. It makes the conversion simple. As already discussed regards to decimal digits conversion, one can prefer this.
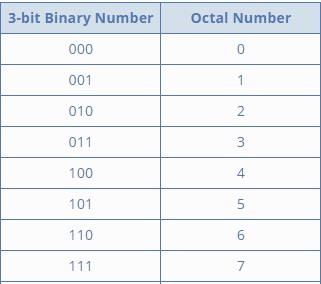
Octal Numbering System Conversion Table
Octal to Binary Conversion
The numbers can be converted from binary to octal even the binary values can be further converted to octal. It is absolutely a reversible process. The important point to be considered while conversion is that each octal must possess three digits of binary. Based on the numbers given in octal are written in terms of powers of 8. Basing on their positions they are converted into binary digits. It becomes very simpler with the help of the conversion table as discussed above.
The other alternate algorithm is to convert the given octal number into a decimal format. Then these decimals can be converted into binary.
Examples
The conversion can be understood in detail with the help of this example.
Convert octal 150 into binary.
By looking at the conversion table of octal to binary 150 can be converted as
1 5 0
001 101 000
Hence 150 in octal can be represented as 001101000.
Convert octal number 270.54 into binary.
Based on the representation of digits in the conversion table, it can be converted as
2 7 0. 5 4
010 111 000 101 100
Hence the octal value 270.54 can be converted as 010111000.101100 into binary.
There are different numbering formats in which each has a specific pattern of representation and applications in various sectors. Coding and decoding can be done through the online tools available. However, the conversion into binary from any other numbering format is necessary because all the digital circuits understand only this format. Can you convert 470.52 that is an octal number into binary?