Binary Numbering System is the simple representation of decimals in terms of ‘0’ and ‘1’. The hexadecimal system is the compact way of representing the decimals. When the large values of decimals are considered the representation of it in terms of binary becomes lengthy. The binary system is based on the position of the digits starts from the right-hand side as its first preferred digit.
This system dependency on the position value makes this system to refer to as ‘weighted or position system’. Both numbering system representations are most convenient, simple to analyze and get converted from one to another. Each has its advantage based on its utilization. Binary systems depend on the representation of the values in the form of ‘0’ and ‘1’. Whereas the Hexadecimal Numbering Systems are depended upon on the decimals from 0-9, further 10-15 are represented by alphabets A-F.
Binary Numbering System Uses
There are various uses of this binary numbering system. Some of them are listed as follows:
- The devices that require the involvement of processors prefers this numbering system.
- To represent the state of the voltage in the circuit follows this system. The value ‘0’ at the input side indicates the OFF stage and the ‘1’ represents the ON stage. Practically this type of requirement is present in the device or the circuit called Switch.
- The Micro-controllers also prefer the logic of binary in the computations.
Hexadecimal Numbering System Uses
For the smaller applications used in the digital world binary system seems to be convenient. It is known for its minimum computational errors. But when the digital system designed is focused on high application orientation. In such cases the conversion becomes lengthy and the system task gets affected due to it.
Further to avoid complexity each digit in the binary is grouped in the form of four. This group represents the half byte of the total value. This system of four grouped digits is another kind of numbering system that is referred to as the Hexadecimal Numbering System. The base of it is represented by the value 16. As for the radix value is 16 this system consists of sixteen numbers in it.
It is a little bit complicated in comparison to the other numbering systems such as decimal and binary. But when dealing with larger systems which requires addressing the locations in the memory to fetch or store data for computational efforts this system is preferred. The presence of two hexadecimal produces the range of bytes from ’00 to FF’.
Binary to Hex Converter
A numerous number of calculators are available online or even a scientific calculator has this factor of converting binary into hex without any extraneous efforts. The hexadecimal system represents the binary with four bits. It starts with the right-hand side. Some of the points to be noted during this conversion are as follows:
Four digits are mandatory for conversion. If that is absent in such case zeroes must be inserted. Suppose if the ‘1’ is represented by ’01’ but in the hexadecimal system it must be represented as ‘0001’.
Let us discuss this in detail with the following example of 1100
- The initial digit at the right-hand side that is 0 it must be multiplied by ‘1’.
- The number next to the initial digit must be multiplied with ‘2’ or ‘2 to the power of 1’.
- The digit present at the third digit multiplied with ‘4’or’2 to the power of 2′.
- The fourth position digit must be multiplied with ‘8’or ‘2 to the power of 3’.
- After performing multiplication add these values to obtain the final hex value.
1*8+1*4+0*2+0*1= 8+4=12
- Hence the 12 is represented as C in the Hex Numbering system.
The above procedure is followed for converting any binary values into hexadecimal. In case if there exists the string of the binary digits. Then in such cases, it must be divided into four bits groups. These groups of four digits are further converted into each term of hexadecimal.
Examples
Let us consider another example for detailed analysis 000100011100 convert this given binary string of digits into hexadecimal.
The first step is to group the digits.
0001 0001 1100
After groupings perform the above method each group must be multiplied with 8421 as shown above and added to obtain the final value. The conversions of these systems are depending upon the following table.
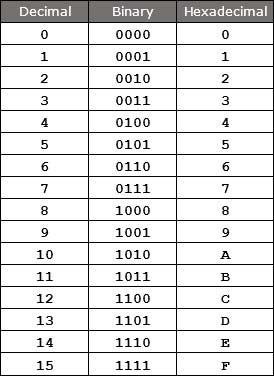
Binary Numbering System to Hexadecimal Conversion Table
By looking at the conversion table we can easily find the numbers.
0001 is represented as ‘1’ in the hexadecimal numbering system.
1100 is represented as C in the hexadecimal numbering system.
Therefore the hexadecimal number for the given binary string is ‘#11C’.
Based on this conversion table or by following the 8421 coding technique many conversions can be done conveniently. The only thing to be noted during these conversions is that digit representation must be of four bits.
For example, if the binary string is 000111 then to convert it into hex grouping is required. That is 00 0111. In this case, the second group doesn’t have four bits. This must be overcome by adding zeroes in that group. Further, the string becomes 0000 0111. Now the conversion is possible. This can be represented as ’07’ in hexadecimal. These are the various techniques utilized during the conversions.
Binary to Hexadecimal Encoder
These systems are usually preferred during the design and the preference of digital systems. However, there is certain logic gates are utilized for these purposes. The conversions have a wide range of applications in the modern digitized world of electronics. An encoding technique is applied at the input stages based on the necessity. These encoders are compressed with various logic gates in it. These are available in the form of ICs.
The basic purpose of this encoder is to convert the binary information into the hexadecimal values. That is, it converts one code into another. There are certain languages in which the programs are written to convert binary into hexadecimal.
Can you convert 001111111100 Binary String into Hexadecimal Numbering Format?