Hexadecimal Numbering System and the Binary Numbering System are used to represent the numbers in the ‘Digital Systems’. The language of all the computational processors which we used in our daily life cannot understand the general words. It can understand only 1’s and 0’s. The words or the programming languages need to be converted to machine languag to make the processor understand the language. The conversion of values from hexadecimal to binary seems to be easier. This is the main reason why many programming languages prefer this hexadecimal system.
The radix or the base of this hexadecimal system is represented by digit ’16’. In case of Binary it is represented by ‘2’. The representation suggests that total terminology in this system is dependent on ‘1’ and ‘0’. Let us discuss in detail about these systems and conversions.
HexaDecimal Numbering System
The numbers that are represented in binary are grouped in terms of four. These four digits of 0’s and 1’s constitute a number in the Hexadecimal Numbering System. This is even preferred in the computers as well as the digital systems. As this is considered to be the system that considers base value as 16, it consists of 16 numbers in it. It is in the range of zero to fifteen. There is an issue with this system because decimals can be represented from 0 to 9. This can be overcome by representing the values 10 to 16 with alphabets ‘A, B, C, D, E, F’.
The number representation starts with LSB (Least Significant Bit) that is from the ‘right-hand side’. To represent these systems or to get it identified from the other different numbers‘#’ and the ‘$’ are used before the value. The example for this is $D4CA or #D4CA. The maximum value represented in the hexadecimal system is ‘FFFF with base 16’. It is equivalent to ‘65535’ in the decimal.
Hexadecimal to Binary Converstion
The numbers in this hexadecimal are referred to as ‘Bits’. Each bit is either represented using ‘1’ or ‘0’ value. The representation of the decimals in this system depends upon its position. Each position is consists of the power raised to the base ‘2’. Its initial representation starts from 2^0 that is from the right-hand side. Hence the dependency of the values on the positions makes this system a ‘Positional Number System’.
For small decimals, it is easier to analyze but for the large values of decimals, the length of its string tends to increase. It is difficult for humans during analysis. In the expression of ‘Boolean Algebra’ and the various ‘Digital Encoding’ techniques, this system is preferably used. On the digital platform of electronics let us consider the example of the switch. It has preferably two states. One is ON and the other is OFF. ON stage is represented by using ‘1’ and the OFF stage is represented by using ‘0’.
The simplest and easiest way of Hexadecimal to Binary is by the representation of each digit into a grouping of four bits. There is no specific hexadecimal to binary converter formula. But based on the fixed chart provided the values are substituted.
The tabular representation of these systems is
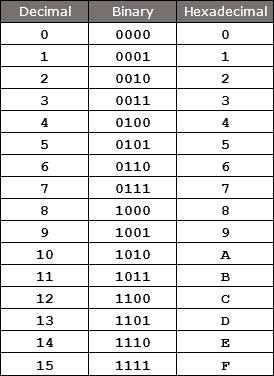
Hexadecimal and Binary Number System Representation
Convert Hexadecimal Value C1 to Binary
C1 is the hexadecimal value where C is the value 12 in the decimal system. The conversion can be done by using the above chart. The ‘C’ representation in terms of binary is 1100 and ‘1’ is represented as 0001.
Hence C1 in hex is equivalent to 1100 0001 in terms of binary. Four bits are considered to be ‘a half byte’. Hence this indicates that the conversion of hex in the binary requires dividing each digit into four bits. The above is considered as one of the examples of this conversion.
Let us discuss this in detail with further examples.
- Convert #4A into Binary
In binary 4 can be written 0100 and A can be written as 1010. Altogether it can be written as 0100 1010.
- Convert 25 Hex into Binary
In binary 2 can be written as 0010 and 5 can be represented as 0101. Therefore it can be written as 0010 0101.
- Convert $1E3 into Binary
In the binary system, 1 is represented as 0001, where E is denoted as 1110 and 3 can be written as 0011. Overall the binary form of this 1E3 is 0001 1110 0011.
Based on the tabular chart of the binary value are shown the given hex values are converted in the form of binary.
Hexadecimal to Binary Encoder
The encoder for this conversion in digital systems is designed by utilizing the NAND logic gates and the IC is also available specifically for this purpose. They can be called as encoder. It takes input as hexadecimal value and the output is generated in terms of four binary bits. In the coding techniques to make the machine understand the instructions, this conversion is needed at the final stage. A decoder is also placed to decode the information. Mostly the 7430 ICs are used for this purpose.
There are various applications of each numbering system. For example, the various representations of colors can be represented by the usage of this hexadecimal numbering system that must possess 6 digits. The binary system is also advantageous because, using it in the programming languages reduces complexity. Even the error during the computations is reduced or minimized. There are various programs written to convert hexadecimal values in to binary. After Conversion it is difficult to understand by humans.
The complements of the numbers can be easily obtained when the value is converted in terms of binary. Hence there are various applications in the digital platform for these types of conversions. The conversions are based on the fixed values provided in the chart. For detection of the electrical signals requires the binary conversion. This is because the state of the signal can be easily understood by fixed values of 1 and 0. The binary values can also be converted to hexadecimal. To know about it click on Binary to hexadecimal convertion. Can you convert #25A into Binary?