Decimal Numbering System is an extension of the Hindu-Arabic Numeral Numbering system. Earlier Counting of larger number was difficult but by the introduction of Decimal Numbering System it became easier. This system is represented with the radix 10 or base 10. This number system came into existence after the invention of zero by an indian mathematician. This is the widely used number system throughout the world.
Likewise in the machine to machine communication or man to machine communication where the information has to be fed in an understandsable format to the computers or any devices that consist of processors and microcontrollers Binary number systems is used. It has it origin in different countries like India, China, Egypt etc. Binary numbering system can be easily implemented in digital circuity using logic gates and so it is machine understandable .
Decimal number system can be converted to binary number and similarly binary number can be converted to decimal number. The numbers in decimal are represented from 0 to 9. The binary numbers are represented as ‘0’ and ‘1’. Encoder are available which can convert one number system to the other which we shall discuss at the end, but now let us convert one number system to the other.
Binary to Decimal Converter
Even though there is availability of Binary to Decimal Converters there are few steps involved if it is to be converted manually. Let us discuss the steps involved behind this with an example.
- The given series of binary numbers are written accordingly. Based on the positions from right to left they are marked in term of increment order of powers of 2.
Example of Binary to Decimal Conversion
1 0 1 1 0 1 1
2^6 2^5 2^4 2^3 2^2 2^1 2^0
- Based on the position of the numbers the power values of respective positions are mentioned.
1 0 1 1 0 1 1
64 32 16 8 4 2 1
- The next step is to multiply the given binary digits with the obtained position values. The same value is written when it is multiplied with the binary value 1. It is written as 0 when it is multiplied with the binary value 0.
- Finally, the resultant number is obtained by summing up the values.
64+0+16+8+0+2+1=91
Hence the final value of the given binary sequence in terms of the decimal is that 91. It is represented as 91 with base 10.
Doubling Method
The other method for converting binary values into decimal is by using a method called ‘Doubling Method’.
The method starts from the position left. The very first digit is considered a number with zero value. This number is doubled by multiplying it with 2 and adds the binary value that is present in that position. It is a chained process. The final value is dependent on the result of the previous value.
Let us consider the same example we have used above.
1 0 1 1 0 1 1
- 0*2+1=1
- 1*2+0=2
- 2*2+1=5
- 5*2+1=11
- 11*2+0=22
- 22*2+1=45
- 45*2+1=91
By using this technique one can convert any base or radix value to decimals.
Decimal to Binary Converter
Example
Convert 150 Decimal into Binary Numbering System
- In the very first step let us divide the 150 with the value 2. The reminder in this step will be 0 followed by quotient is 75.
- The resultant 75 is further divided by 2. In this case, the reminder will be 1. Because the quotient obtained is 37.
- Further 37 are divided by 2. The quotient obtained is 18 and the reminder is 1.
- Then 18 on dividing by 2 results in quotient as 9 and the reminder will be 0.
- Further on dividing 9 with 2 the resultant reminder of it is 1 and the quotient is 4.
- 4 when divided by 2 results in the reminder as 0 and quotient as 2.
- Finally, when 2 are divided with 2 the remainder is 0 and the quotient is 1.
The process stops when the quotient is obtained as 1. Then the binary value obtained is written as 10010110. The values are written from the final reminder to the reminder obtained in the first step. This can even be verified by using the above binary to decimal process. One important point to be noted from the above division is that when the quotient obtained is odd the reminder obtained as 1. Otherwise, the obtained reminder is 0. There are other methods of conversions. But the division method is simple to understand and analyze.
Binary to Decimal Table
The below table consists of the values of decimals and the way they are represented in binary. By remembering these table values or looking at the table one can also do the conversions easily.
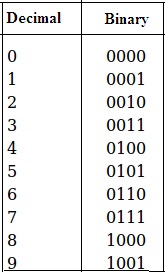
Decimal Numbering System to Binary Numbering System table
Encoder
In the digital systems where the chips are to be mounted and the conversion should be done automatically the ICs are designed which are known as the encoder. The purpose is to convert the one numbering system format into another based on the requirements.
Know more about Binary Division MCQs.
Generally, the most utilized numbering format is decimal. This is the human-understandable system. But the other formats are used based on requirements in the digital circuits or systems. Can you convert 250 Decimal numbers into Binary?