Quine McCluskey minimization method, is a technique for reducing for minimizing the expression in their SOP (sum of product) or POS (product of sum) form. Also called a tabular method, this method has advantages over the K Map method, in case the number of input variables is large. For an input variable greater than six, the K Map method becomes more complex. For such problems, McCluskey or Tabular method has a simplified approach. Even it has a simplified approach as compared to other techniques such as the Boolean algebra method of minimization. The McCluskey method can be used to design complex circuits in digital systems.
What is Quine McCluskey Minimization Method?
Quine McCluskey minimization method is a method to minimize the Boolean expression in the simplified form. Before, implementing a logic circuit, it is important to note that, the output expression must be in simplified form. Quine McCluskey method is used to simplify boolean expression with more than 6 input variables. The technique is also based on an automatic or computer-driven simplification routine.
Quine McCluskey Algorithm
Before going into the tabular column algorithm for reducing the binary expression, let’s briefly check the important terminology required during the minimization process.
Prime Implicant and Essential Prime Implicant Terms
Implicant is defined as a group of ones, and prime implicant is the largest possible group of ones. Essential prime implicant is the prime implicant having at least one min-term which cannot be combined in any other way. This means that the essential prime implicant is represented in minimized form, which cannot be combined further.
Binary Equivalent of Numbers
Before, moving to Quine McCluskey Algorithm, it is important to remember the binary equivalent of numbers 0 to 15, for quick substitution in the tabular method. The binary equivalent of numbers is given below.

Binary to Decimal Equivalent
The decimal equivalent of the binary representation can be verified, by multiplying each with the weightage of the powers of two. The rightmost bit is called LSB(least significant bit) and the leftmost bit is called MSB(most significant bit). In order to obtain the decimal equivalent, the LSB is multiplied with two to the power zero, then to the power one, and so one. An example depicting the same has been shown below.

Binary to Decimal Conversion
Quine McCluskey Tabular Method
Now, lets see the Quine Tabular method, with an example.
Minimize the following
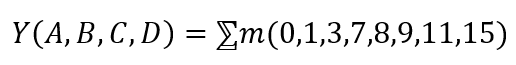
In the above problem, we need to minimize the expression of (A, B, C, D) consisting of the given minterms. It can be seen that A is the MSB and D is the LSB term. We can see one more thing, the highest minterm is 15, which means that the number of variables is four. We can check the binary representation of the minterms from the table given before. Now we will check the step-wise solution of the above problem.
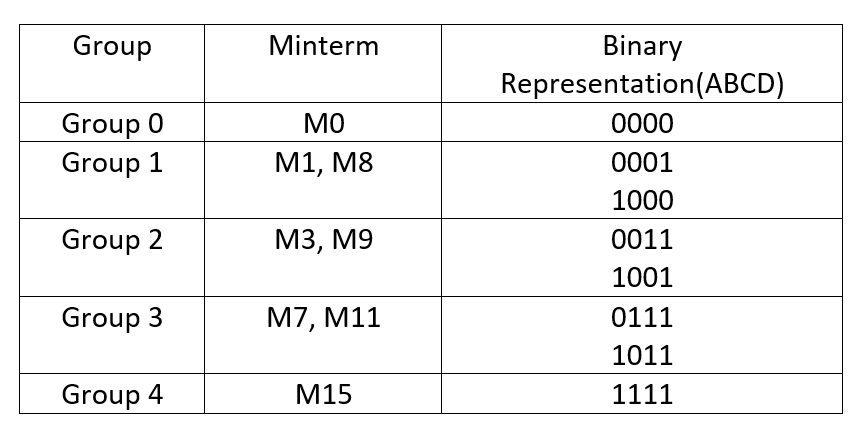
Step 1: For the first step, we need to group all the binary equivalent of the numbers 0-15, based on the number of ones, in their binary equivalent representation. For example, in the binary form representation of 0, (0000), we have zero number of ones. Check the following table.
Quine McCluskey Method
We can see that group 0 has zero number of ones. So 0000 is eligible for that. For group 1 we need one number of ones. So the eligible minterms from the given problem are M1 and M8. For group 2, we need two ones. So the eligible minterms are M3 and M9. Next for group 3, we need three numbers of ones. So the eligible minterms are M7 and M11. In the last group, we have one more minterm M15 which consists of four ones. So dividing the given minterms based on the number of ones is the first step.
Step 2. Before going to step 2, we need to understand what is a Matched Pair. Two numbers are said to be in matched pair if they differ with only one digit. For example, from the eligible minterms, if we check that for the minterm M0 and M1, (0000-0001), we can see that they differ with only the last one digit.
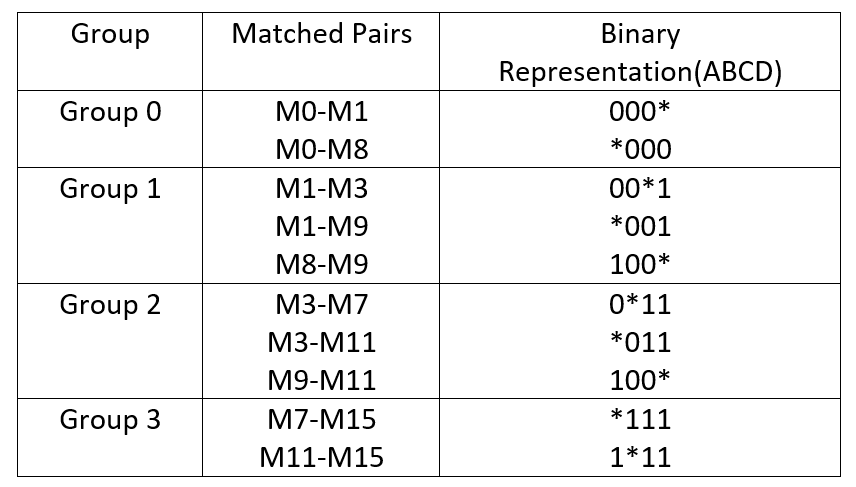
So they are qualified as matched pairs. Similarly, we need to check for all groups. The rule for selecting a group is n and n+1 group. This means that 0 groups are checked for matched pair for group 1, the group is to check with group 2, group 2 with group 3, and so on. Based on that, the following table is formulated.
Quine McCluskey Tabular Method
As we can in the first group, the matched pair is (M0-M1) and out of which the last digit is different. So it represented with a *. Similarly, while comparing group 0 and group 1, we can see that M0 and M8 also differ by the first digit, (0000-1000), so that is replaced by * in the binary representation. Next, we will compare, group 1 with group 2.
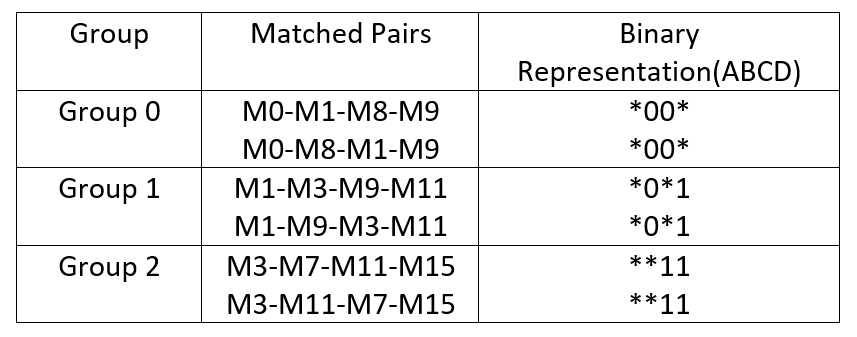
Step 3. In the next step, we will now find the matched pairs, as we did in the previous step, out of the matched pairs we found in the previous step. For example, if the check for matched pairs (M0-M1) and (M1-M3) they are given as (000* and 00*1). We can see that the last two digits are changing. So they cannot be termed as matched pairs. Similarly, if we compare (M0-M1) with (M1-M9) then we have (000* and *001). Again two bits are differing. So they have not matched pairs. In this manner, we will fill the table.
Tabular Method
But if we compare the group (M0-M1) with (M8-M9), then we can see that representation is (000*) and (100*). So only the first bit is differing. The rest three bits are the same. So they are qualified as matched pairs. Similarly, we can complete the whole table as shown.
Step 4. Again the same step is repeated to find out the matched pair between group 0 and group 1 as obtained in step 3. But we can see that further, we can’t find any matched pairs between the groups 0,1, and 2. Therefore we can now write the minimized form
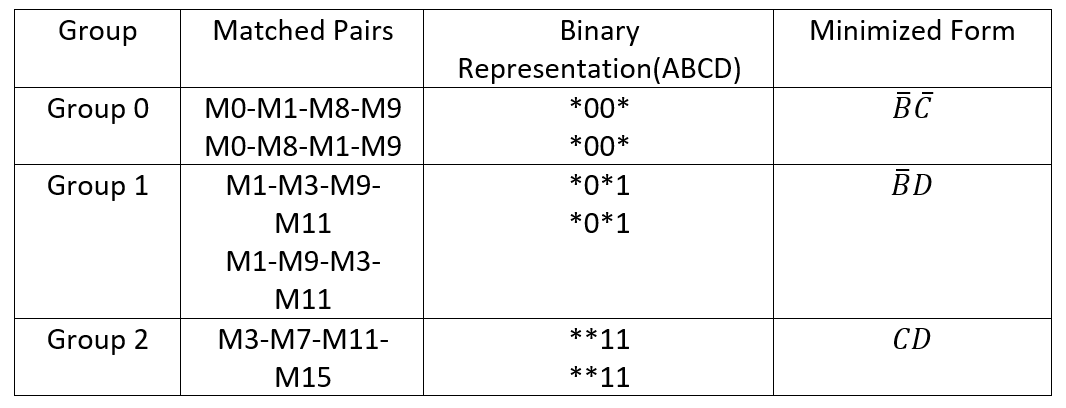
Quine McCluskey Minimized Form
From group 0, we can see that the variables A and D are eliminated. Only B and C are left. If it is 0 we represent it with a compliment. If not, they are represented with a normal variable So the prime implicant is obtained in the last column.
Step 5. Now the next step is to obtain the essential prime implicants out of the prime implicants obtained in the previous step. For that consider the following table.

Minterm Minimization
From the prime implicants, we can check the minterms involved. Like for the first one the minterms involved are (0,1,8,9), and we will put across if it appears in the minterm given in the problem. Then we need to identify by putting a circle if that minterm is appearing only once.
So the minterm involved in the second row (1,3,9,11) are not essential prime implicants. Since each of them has already appeared in the first or third row. So finally the minimized expression can be given as
![]()
Hence we have seen, how to obtain the minimized expression by using the Quine McCluskey method. The same procedure can be checked for a problem involving 5 or 6 variables.
Quine McCluskey Method Advantages and Disadvantages
The best advantage of the Quine McCluskey method is, it can be used to minimize the expression of any inputs, which is not so easy using K-maps. For this reason, generally, it is used for variables involving 5 or above. But the disadvantage is complexity involving as we need to tabulate 4-5 tables in order to find the minimized expression. Which may cause, errors while calculating.
Please refer to this link to know more about De-Morgan Theorem MCQs.
Please refer to this link to know more about Quine Mccluskey Method MCQs
We have seen Quine McClusky’s method of minimization, along with steps for the solution and solved examples. The same methodology can be adapted with a higher number of variables. Also termed as the tabular method, this method can be used for minimizing boolean expression with variables of more than 5. This method also checks out prime implicants and essential prime implicants for a given expression.