In network analysis, the basic and simple circuits can be analyzed by using basic techniques and laws like KVL, KCL, and ohm’s law. In the case of complex circuits, these laws are not applicable and unreliable as it consists of controlled sources. Hence to find the variables in complex circuits, mesh, and nodal analysis techniques are used. By the use of mesh/loop and nodal analysis, we can determine the variables like current and voltages of the circuit very easily. This nodal analysis is used to determine the amount of current flowing through the branch in a circuit. It is also known as the loop analysis method or mesh current method. This article is about an overview of mesh analysis and its examples.
What is Mesh Analysis?
The method that is used to determine the current flowing around a mesh or loop in the closed complex circuits is known as mesh analysis. It is also called a mesh current analysis or loops current analysis. It makes use of Kirchhoff’s voltage law and ohm’s law to determine the unknown current flowing in a given complex circuit. For planar circuits, this analysis is very easy to use. We can find the unknown voltages in a given circuit using ohm’s law. It is also known as loop current analysis or mesh loop analysis or branch current analysis or mesh current method.
It is similar to the branch current method, in which Kirchhoff’s voltage law and ohm’s law are used to determine the unknown current in the given circuit. The main advantage of using the mesh current method is, large networks can be solved with few unknown values and mesh equations. For example, the branch current method takes 3 equations while the mesh current method uses only 2 equations to solve the complex electrical circuit. If the resultant equation is negative, then the assumed direction of the current is the circuit is negative. The mesh current analysis or mesh loop analysis is very easily used to solve the voltage and current sources in the planar circuits.
Mesh Analysis Steps
The path that joins two nodes, which contains circuit elements is known as a branch. The current in the branch is equal to the mesh current only when the branch belongs to one mesh. The sum/difference of two mesh currents is equal to the branch current when the branch is similar to the two meshes. The direction of these currents will be the same or the opposite. The following are the different steps involved in solving a complex electrical circuit or network.
- Recognize the meshes and label the direction of mesh currents ie., anticlockwise or clockwise directions.
- The next step is, the amount of current flowing through every circuit element is observed and noted in the form of mesh current.
- Apply KVL and ohm’s law to write the equations for all meshes.
- To obtain the value of mesh currents, solve all the mesh equations obtained before.
- Hence by following the above steps, it is very easy to determine the current that flows through each element and the voltage that is present across the element in the circuit or network
Mesh Current Method
The mesh current method explained by considering some of the mesh analysis problems and examples of an electrical circuit or network.
The below electrical circuit explains all the details about the problems & examples, mesh analysis solved problems, and mesh loop analysis examples.
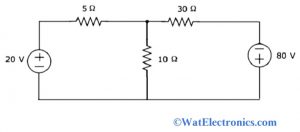
Mesh Current Method
Consider an electrical circuit with resistors and voltage sources as shown below. Now, using this analysis we have to obtain the voltage across the 30 ohms resistor. This example explained in finding the current in the circuit using the mesh current method.
Step I: From the given circuit, we observe two meshes with mesh currents I1 and I2 in the clockwise direction. The circuit with the mesh currents is shown below.
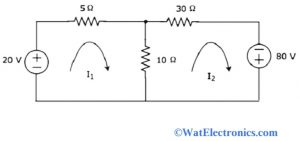
Mesh Loop Analysis
Step II: Consider the mesh current I1 flows through the voltage source of 20 volts and resistor of 5 ohms. At the same time, I2 is considered as the mesh current flowing through a 30 ohms resistor and -80 volts source. The current flowing through the 10 ohms resistor is the difference between two mesh currents I1 and I2.
Step III: Solving two meshes using mesh current analysis
Determine all the mesh equations for all the meshes in the given circuit.
To write the mesh equation, consider the mesh current of one mesh is greater than all other mesh currents of the given circuit.
For the first mesh, the mesh equation is written as,
20 – 5 I1 – 10( I1 – I2) = 0
20 – 15I1 – 10 I2 = 0
10 I2 = 15 I1 – 20
By dividing the above equation by 5 we get,
2 I2 = 3 I1 – 4
By multiplying the above equation with 2 we get,
6 I1 – 8 = 4 I2 ………….eq 1
For the second mesh, the mesh equation is written as
-10 ( I2 –I1) – 30 I2 + 80 = 0
By dividing the above equation with 10 we get
– ( I2 –I1) – 3 I2 + 8 = 0
– 4 I2 + I1 + 8 = 0
I1 + 8 = 4 I2 …………..eq 2
Step IV: Finding current in a circuit using mesh current method
Obtain the I1 and I2 mesh currents from the above eq 1 and eq 2
By equation the above two equations we get
6 I1 – 8 = I1 – 8
5 I1 = 16
I1 = 16/5 Amp
To obtain the mesh current I2 put the value of I1in eq 2
4 I2 = 16/5 + 8
4 I2 = 56/5
I2 = 14/5 Amps
Hence by applying mesh loop analysis and mesh current method, the mesh currents I1 and I2 are determined.
The mesh current I1 across 20 volts and 5 ohms is 16/5 Amps
The mesh current I2 across -80 volts and 30 ohms is 14/5 Amps
Step V: By applying ohm’s law, the voltage across the resistor 30 ohms is determined
V at 30Ω = I2 R
By placing the value of I2 and R we get
V at 30Ω = 84 Volts
Hence the voltage across the resistor 30 ohms is obtained as 84 Volts
The same procedure is followed in solving three meshes using mesh current analysis.
Super Mesh Analysis
This analysis method is better as compared to mesh analysis of a complex electrical circuit with the current source as a common element for all the meshes in the given circuit.
When two meshes having the current source as a common element then a super mesh is formed. In this analysis, the current source will be present inside of the super mesh. Hence the no. of meshes can be reduced by one for every current source that is present in the given complex network. We can ignore the single mesh if the current element is placed on the perimeter of the electrical circuit.
We can define the required mesh equations using KVL and KCL to solve the mesh currents in the circuit.
Example
Super mesh analysis is used when a current source is in between the two meshes. It is necessary to check whether the given circuit contains a current source or not. By incorporating two mesh currents, one mesh equation is formed, which relates to the current source. The current source in the resultant mesh equation is equal to one of the mesh currents minus the other. This method is better than mesh analysis to solve complex electrical circuits.
To solve the super mesh analysis example, it is necessary to follow some of the steps as discussed below,
- Check whether the given circuit is planar or not
- To simplify the circuit, redraw it
- Identify all the possible meshes in all the loops to find the mesh currents. Label the direction of the meshes ie., clockwise or anticlockwise direction
- Using the common current source element, analyze how to draw a super mesh
- Apply KVL and KCL to the above super mesh
- Solve all the mesh equations to determine the mesh currents
The below example shows finding current in a circuit using the mesh current method. This example also includes in solving the two meshes using mesh current analysis
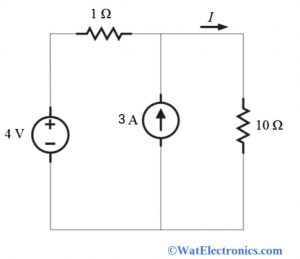
Example on Supermesh Analysis
From the given circuit, we can observe that the current source of 3Amps is connected between the two meshes.
Step I: the no. of meshes formed in the given circuit is 2
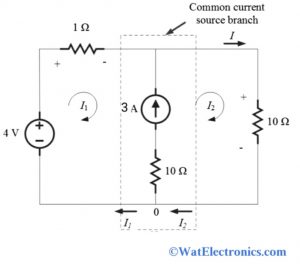
Meshes Formed in the Circuit
Step II: let the mesh current I1 flow through the first mesh and mesh current I2 flows through the second mesh. We can ignore the current source 3 Amps, which is connected between the two meshes
Step III: redraw the circuit as a super mesh by ignoring the current common current source
Step IV: determine the mesh equations for the above super mesh circuit by applying KVL
By applying KVL to the super mesh we get,
-4 + I1 + I2 + 3 = 0
I1 + I2 = 1……………eq 1
By applying KCL at node 0 we get,
I2 – I1 = 3
I2 = I1 + 3……………eq 2
Substitute eq2 in eq1 then,
I1 + I1 + 3 = 1
2I1 + 3 = 1
I1 = 1 Amp………..eq 3
From eq 1
I1 + I2 = 1
Substitute the value of I1 in the above eq 1
1 + I2 = 1
I2 = 0
I = 1 Amp
Hence the total current flowing through the super mesh is 1 Amp
Applications/Uses
Mesh analysis uses includes,
- Solving of complex electrical circuits or networks to determine the unknown sources like voltage and current with possible mesh equations
- Simplifies the complex circuit
- Reduces the mathematical equations with simplified calculations to solve the circuit.
- Analysis of complex circuits or networks
- Determines the unknown current or mesh current, which flows through the meshes in the given circuit
- Uses KVL and KCL to find the set to mesh equations to solve the circuit.
- It is applicable only in planar circuits
Please refer to this link to know more about Nodal Analysis MCQs , Mesh Analysis MCQs
Thus, this is all about an overview of the mesh analysis used for solving the complex planar electrical circuit– definition, mesh current method, steps involved in mesh analysis, mesh analysis problems & examples, mesh loop analysis examples, super mesh analysis, example on super mesh analysis, finding current in a circuit using mesh current method, solving two meshes using mesh current analysis, solving three meshes using mesh current analysis and mesh analysis uses. Here is a question for you, “What are the advantages and disadvantages of mesh analysis?”