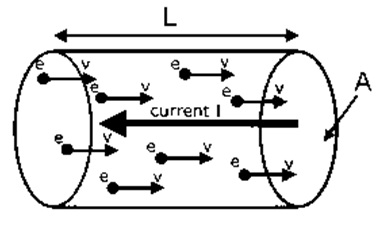
The drift velocity concept can be understood by observing the random movement of electrons around the conductor. These electrons keep on traveling in the conductor in a random way through random velocities. Sometimes, a conductor may be subjected to an electric field & consequently some type of electrical energy is used on the randomly moving electrons except in the field direction.
This field pushes the electrons to control in the high potential direction while maintaining their chances of motion. Thus, we have noticed that each charge carrier will include a certain net velocity through which it will move in the way of the conductor’s maximum potential end. So this net velocity of the electrons is called the drift velocity. This article discusses an overview of drift velocity.
What is Drift Velocity?
Drift velocity definition is, subatomic particles like electrons shift in random ways continually. Once electrons are subjected to an electric field then they shift randomly, however they drift slowly in one way within the direction of the applied electric field. The net velocity at which point electrons will drift is called also called drift velocity. To understand this concept first we have to know about drift. So, drift is the movement of an object slowly in the direction of something. The SI unit of drift velocity is m/s or m2/(V.s).
Drift Velocity
In a resistive material, this is directly proportional to the current as well as the magnitude of the exterior electric field. Based on ohms law, the drift velocity equation can be expressed as
u = µE
From the above-mentioned equation,
‘u’ is the drift velocity
‘µ’ is electron mobility
‘E’ is the electric field
Drift Velocity of an Electron
Once the average velocity is achieved by electrons particles in the electric field are called the drift velocity. We can imagine that the movement of particles will be through a plane & thus the motion can be expressed like the axial drift velocity.
This concept is understood through revising the electron’s random motion around the conductor. In a conductor, the movement of the electrons will be continuous within a random manner using random velocities. Once the conductor is in the electric field then some force is applied toward the moving electrons within the field’s direction.
Drift Velocity of Electrons
Here, this field pushes randomly moving electrons to switch in the direction of high potential when maintaining the possibility of the motion. Scientifically, we can state that the randomly moving electrons will drift in the direction of high potentials by keeping random motions.
Further, we can notice that when the electron moves toward the high potential end of the conductor then it has its own velocity. So the net velocity of electrons is called drift velocity. In the conductor, the current which is generated because of the electron’s drift movement is called drift current. The flow of current within the conductor is called drift current.
In a conductor, whenever the charged particles move around by colliding with other particles. Thus, the particle’s average speed can be taken into observation within the conductor. Under the electric field impact, the average velocity can be obtained through the electrons because of the electron’s drift.
It can be calculated through current density, so the formula is given as
V = 1/nAq
In the above-mentioned equation where,
‘V’ is the drift velocity of electrons
‘I’ is the flow of current in the conductor that is measured in Amperes
‘A’ is the conductor’s cross-section area that is measured in m2
‘q’ is the electron charge, measured in Coulombs
‘n’ is the number of electrons
So, from the above drift velocity formula, we can conclude that, from the out of 4 quantities, any three are given then the remaining quantity can be found out simply. Thus, the electron’s velocity within a specific metal piece showing 0.1 Amps of current is approximately 1×10-5 m/s. Usually, the electrons shift at extremely high speeds like million m/s throughout a wire however, they move extremely slowly within the path of the current. So this is an example of drift current.
Derivation
Electrons within the conductors move in random ways which cause a collision between them. The flow of current can be caused once all the electrons present in the conductor shift in a specific direction.
Now, there is no specific time once these collisions occur in a conductor, assume that the time among the clash of electrons is ‘T1’. Likewise, for the second time, ‘T2’ is the second pair of electrons & this will continue for all the electron pairs which are there in a conductor.
For instance, assume the whole number of pairs like ‘n’ thus we will analyze an average from T1 – Tn which is known as Relaxation time (乁). It can be defined as the time period between the collisions of two electrons.
Relaxation time formula (T) = (T1+T2+…Tn)/n
We already know that, V = U + at
From the above equation
‘ V’ is the final velocity
‘U’ is the initial velocity
‘a’ is acceleration
‘t’ is time.
If early velocity like U is 0 after that, V = at
So we know the acceleration like m = F/m = -Ee/m
We know that.
V1 = -Ee/m . T1 & Vav = Ee/m T
This average velocity is because of the application of electric field (E) within a single direction.
Drift velocity = Vd = -Ee/m T
In the above equation, ‘Vd’ mainly depends on the electric field & the Relaxation time ‘T ‘.
Relation between Current Density & Drift Velocity
The current density can be defined as the whole current supplying throughout a cross-sectional conductor unit within a unit of time. We know the formula of drift velocity.
V = 1/nAq
From the above equation, we can write is as
I = nAvQ
J = I/A = nVQ
Where,
;J’ is the density of current measured within Amperes for each square meter
‘v’ is the electron’s drift velocity
Therefore, we can conclude that the electron’s velocity & its current density is equivalent to each other. In addition, once the intensity of the electric field enhances, then the velocity will be increased & the flow of current throughout the conductor also enhances.
Relation between Electric Current and Drift Velocity
The current ‘I’ for a conductor can be derived as
I = nAvq
From the equation,
‘A’ is the cross-section area of the conductor
‘n’ is the number of charge carriers for each cubic meter
‘q’ is the charge on every charge carrier
‘v’ is the charge carriers drift velocity
For electron, I = nAve, where the electron charge is ‘e’
This equation may be deduced as follows, with reference to Figure a:
If we notice a part of the length of wire that is Δx
The volume of wire within the section will be
ΔV = AΔx
If the charge carriers are ‘n’ for each unit volume within the wire, then the number within volume ‘ΔV’ will be
ΔN = n*ΔV = n*AΔx
On every charge carrier, if the charge is ‘q’ then the charge quantity in the section will be
ΔQ = nAqΔx
Assume that every charge carrier takes a time ‘Δt’ to move the distance ‘Δx’.
If the above equation is Divided through Δt at both sides, then
ΔQ/Δt = nAq Δx/Δt
Here, ΔQ/Δt = I & Δx/Δt = v, so I = nAvq
So this is the relation between the current & the velocity.
Relation between Drift Velocity and Electric Field
The main relationship between the electric field & drift velocity is discussed below. The magnitude of this velocity is ‘m’ for each unit electric field is derived as
m = |Vd |/E => qt/ m
The SI unit of mobility is m2/Vs where mobility is a +ve quantity.
Vd = mE
So the above-mentioned equation is the main relation between an electron’s velocity & the electric field.
Relation between Drift Velocity and Relaxation Time
The main relation between drift velocity & relaxation time of electrons within a conductor is discussed below. A conductor with ‘L’ length is connected to a direct current and the emf source is ′E′. If the conductor’s length is increased through extended it, keeping emf source stable, then this velocity is affected.
The electrons drift velocity is vd = at/2
Electrostatic force can be given through ma=qE′
vd=qE′τ/2m
Where E′=E/L
So, length is extended while maintaining potential disparity is stable.
The new electric field can be specified throughout E′′=E/3L=>E′/3
Thus, v′′d = vd/3
So, drift velocity will turn into 1/3rd.
Please refer to this link to know more about Ohms law MCQs.
Thus from the above information finally we can conclude that the equation of drift velocity ‘Vd’ mainly depends on electric field (E) & relaxation time (T). If the temperature enhances then the relaxation time will reduce, so this velocity will be reduced. So, relaxation time is stable for a stable temperature. So, this velocity is not dependent on the time at a stable temperature. here is a question for you, what is a diffusion current?