The capacitor is an energy storage device. These are classified as Electrolytic and Non-Electrolytic Capacitors based on the Dielectrics and Polarities. It must be connected in the circuit in such a way that a required value of the capacitance is obtained. There are other combinations of capacitors used during connecting it in the circuit. Among which series and parallel are the basic ones.
The multiple capacitors that are connected acts as the ‘Single Equivalent Capacitor’. The total amount of capacitance in a ciruuit on the number of individual capacitors connected in series in circuit and would be less than the any one of the capacitor in the circuit. The spacing between the plates of the capacitor also affects the capacitance of the capacitor.
In the power distribution systems where the level of voltages gets to fall below the level specified. These components called capacitors are used to maintain the line of voltage. These components can minimize the loss of power. With the basic series and parallel combinations, further complicated connections can be derived.
What is Capacitor in Series?
The connection made in between the capacitors placed in one single line can be defined as capacitors connected in series. The plate of positive charges of one capacitor is connected to another capacitor plate of the negative charge. In this type of connection, each capacitor has equal amounts of charge value and the Charging current.
Even though the charging current is the same but it differs at the voltage drop. Each capacitor has different drops of voltages. But the overall voltage drop that is applied between the input and the output lines is the same as the sum of the voltages of the individual drops.
Capacitors in Series Working and Equation
The capacitor connected in a series usually possesses less amount of capacitance. When these connections are made the current flowing through the circuit is the same. Hence the charge stored around each of the capacitors is also the same.
Capacitors Connected in Series
Usually, the capacitors are connected in a ‘daisy chain’ configuration. In such kinds of circuits, the flow of current for charging will be equal. This is because of the path establish is the same.
Total Current = Current at C1 = Current at C2
Instead of capacitance, the charge in each capacitor is the same. Because the plates of each capacitor are connected in an adjacent manner.
Total Charge = Charge at C1= Charge at C2
When the capacitors follow the series connection and more than three capacitors are connected. The C1 is provided with the supply and the C3 will be connected at the output end. Whereas the C2 in the middle is isolated from the direct interaction of voltage supply(DC). Due to this, the voltage drops across each capacitor are different. It depends upon the individual capacitances of each capacitor.
Generally, the charge, capacitance and the drop of voltage are related as
Q=CV
The formula can be rewritten as
C=Q/V
The voltage across capacitors can be calculated as
Total Voltage = Voltage at C1 + voltage at C2
Total Voltage (Q/C) = Q1/C1 + Q2/C2
In Series, the charge will be equal that is Q1=Q2
Finally, on dividing the equation with Q on both sides
1/C = 1/C1 +1/C2
Hence the above equation is to calculate the capacitance for the series connection of capacitors.
Example
The two capacitors connected in series of values 10 microfarads and 20 microfarads. Find the value of capacitance in the circuit?
solution: Given C1= 10 µf
C2= 20µf
The total capacitance can be calculated by the reciprocal of individual capacitances.
1/C = 1/10 +1/20
1/C = 0.15 microfarads
What is the Capacitor is in Parallel?
As there are two plates in the capacitors the first plate of the capacitor is connected to the first plate of the second capacitor. This is known as capacitors in parallel. Therefore, the capacitors in the parallel connection possess the same amount of voltage values. The total value of capacitance is the sum of the individual capacitances.
Capacitors in Parallel Working and Equation
When the capacitors are connected in parallel. Each of the capacitors in the circuit has direct interaction with the conductor. This results in the potential of the capacitor to remain the same. The charge will be as same as that of each capacitor is having an individual connection with the provided supply.
The value of the total charge can be calculated by the sum of the individual charges.
Total Charge (Q) = Q1+Q2+…….
If two capacitors are connected in a parallel manner.
Then, Q = Q1+Q2. Where Q= CV
CV= C1V1+C2V2
In parallel combination V= V1= V2
CV = (C1+C2)V
Therefore, C= C1 +C2
Example
Find the value of total capacitance if the two capacitors of 10 microfarads and the 20 microfarads are connected in the circuit?
Solution:
Given C1= 10 microfarads
C2= 20 microfarads
In the parallel combination, the total capacitance can be calculated as
C= C1+C2
C= 10 + 20 =30 microfarads
Based on the above formulae the value of capacitance can be calculated.
The capacitors can be connected in the combination of series and parallel. During those situations, the connection must be identified. Based on the identification suitable formulae of series and the parallel combination are used.
Example
Find the value of capacitance where three capacitors of 10 microfarads are connected in the circuit?
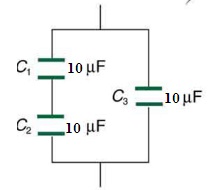
Capacitors in Series and Parallel Combination
Solution:
Given the above circuit consists of C1, C2, and C3 Capacitors.
From the circuit analysis the capacitors C1 and C2 are in series combination.
The C1 and C2 equivalence capacitance can be calculated by using the formula
1/C = 1/C1 +1/C2
1/C= 1/10 + 1/ 10
1/C= 2/10
Finally, C= 10/2 = 5 microfarads.
Further, this C is connected in parallel with the capacitor C3.
The Equivalence capacitance of the circuit can be found by
C (Total) = C+ C3 = 5 + 10 = 15 microfarads
Please refer to this link to know more about Capacitors MCQs
Hence the value of the capacitance can be realized based on the series and parallel analysis. It is noticed as the value of the capacitance is decreases in terms of series combinations. In the parallel combination, the value of capacitance is increased. But in case of resistance, it is the opposite. From the above analysis can you determine if you have to store a huge amount of energy then which combination of connection is preferred?