In electronics circuits, the signal is associated with an AC (Alternating current) and DC (Direct Current). The sinusoidal wave or sine wave represents the periodic AC signal that varies with time and fluctuates between positive and negative cycles. While DC signal/waveform represents the magnitude of voltage and current values easily and stable. But the magnitude of the current and voltage values of the AC signal should be calculated by using its instantaneous values, a peak value of the signal, peak to peak value, average value, and RMS voltage. This article describes the RMS voltage theory and its methods.
What is the RMS Voltage?
The term RMS stands for “Root Mean Square value”. The RMS value represents the voltage value of an AC signal equivalent to the DC voltage. The amount of power dissipated or heating effect is the same in both AC and DC signals. The values of a sinusoidal signal vary with time because the magnitude of the current and voltage values always change with time and it is not applicable for DC circuits (magnitude constant).
In simple words, it can be defined as the square roots of the average values of the squares of all the instantaneous values of an AC signal. It is denoted by Vrms or Irms
This can be obtained by squaring the input values and calculating the average value of an AC signal. The square root of the average value obtained gives the root mean square voltage.
RMS Voltage Theory
In general AC and DC signals are represented in the form of voltage or current waveforms. We knew that the magnitude of the DC signal is constant and it is very easy to calculate. But the AC signal fluctuates between negative and positive half cycles and varies with time. So, it is difficult to find the magnitude of the voltage and current values of the alternating waveform. This theory can be explained from the alternating waveform as shown below.
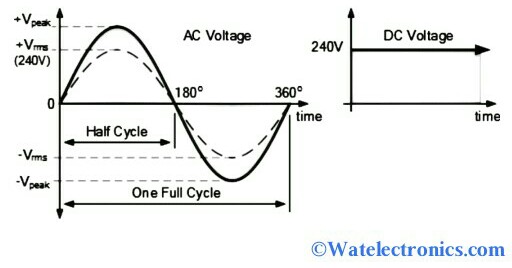
RMS Voltage Theory
The most effective method to find the magnitude of the voltage values of the sinusoidal waveform is the calculation of RMS Voltage value. We can compare the amount of power of AC and DC signals given to the load or circuit. This voltage refers to the DC equivalent voltage of an AC signal because the amount of power dissipated or heating effect of both AC and DC waveforms in the given circuit is the same.
That means the power delivered to the load of a DC is equivalent to the RMS voltages of a sine wave (AC signal). This gives the effective voltage value and it is denoted by Veff or Ieff. If the supply voltage is 220V-240V, then the RMS voltage values of an AC are also 220V-240V, which is equivalent to the power of DC voltage.
If the RMS voltages of AC and DC signal are the same, then the amount of power dissipated in the circuit is also the same. This is also known as an effective voltage which is equivalent to the DC voltage in providing power to the circuit.
RMS Voltage Equivalent
RMS voltage refers only to the AC voltage of a sine wave because it varies with time. That means the magnitude of the AC voltage varies with time. While it is not considered in DC circuits because its magnitude is constant. The process of determining the average value and the RMS voltage value is similar. The complex sine wave of this voltage can be determined by using two methods such as graphical method and analytical method.
Graphical Method
It is also known as the mid-ordinate method. The RMS voltage of a sine wave can be found by simply drawing mid-ordinates on to the given AC signal as shown below. Or we can use the instantaneous voltage values of the given sine wave. This method is very effective to find the values of the RMS Voltages of all types of complex signals.
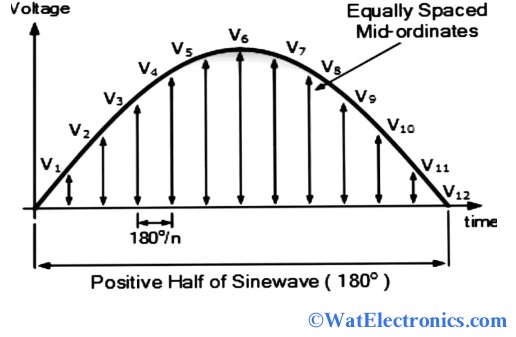
RMS Voltage Graphical Method
Consider the positive half cycle of the given sine wave (AC waveform). Since the process of finding the RMS voltage values is the same for both negative and positive half cycles of the AC signal. In any AC signal, all the instantaneous voltage values on time durations and varies with time. The RMS voltage or effective voltage can ve found by taking instantaneous values of the AC signal.
Draw the mid-ordinates on to the waveform with equal portions of ‘n’ time intervals accurately. The width of the mid-ordinate refers to n° whereas the height of the mid-ordinate represents the instantaneous voltage values.
Let the instantaneous voltage values of the AC signal be V1, V2, V3, V4,…,Vn for ‘n’ no.of time intervals. For example, at t=1 (mid-ordinate drawn at an instance t=1), the instantaneous voltage value will be V1.
By squaring all the instantaneous voltages we get,
V₁², V₂², V₃², V₄², V5²,….Vn²
The RMS voltage of an AC signal is the square root of the squares of all the instantaneous voltages divided with the no.of mid-ordinate. By dividing the no.of mid-ordinates we get the ‘mean’ value of the RMS. Calculate the average of ‘Vn’ values for an ‘n’ time durations.
The MS voltage can be calculated by using the formula as given below,
Vrms = √sum of mid – ordinate (voltage)2/no. of mid – originates
Vrms = √V²₁+V²₂+V²₃+V²₄+V²5+…+Vn²/n
Where V²₁, V²₂, V²₃, V²₄, V²₅,…Vn²are the values of the instantaneous voltages
n is no of mid-ordinates drawn along the ac waveform with time
The average values of the voltage would give the accurate RMS voltage values of the periodic waveform.
Analytical Method
It is a simple mathematical method to find the values of the RMS voltages of periodic waveforms. This method is very easy when compared to the graphical method. It deals with only pure sine waves. The portion under the curve of the sine wave (AC signal) can be analyzed by calculating RMS voltages mathematically.
The expression for constant voltage of periodic AC signal is given as,
V(t) = Vmcos (ωt)
since ω = 2π/T
T= time period
Therefore the RMS voltage of the sine wave can be determined by using,
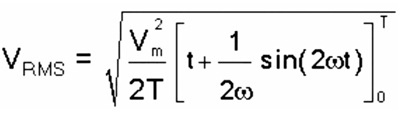
VRMS
To complete one cycle, the integration limits will be 0° to 360° i.e Lower to higher
Then the RMS voltage is given as
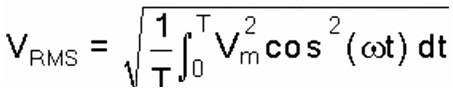
RMS Voltage
The above complex equation can be simplified by using ω = 2π/T
Then we get
Equation
The RMS voltage equation is calculated by using the peak voltage, peak to peak voltage, and the average voltage values of the periodic AC signal.
Peak Voltage
The RMS voltage of a sine wave can be obtained by multiplying peak voltage values by 1/√2 or 0.7071. That means the alternating signal is 1/√2 times the peak voltage values.
Vrms= Vpeak* (1/√2)= Vpeak*0.7071
It refers to the effective values on the signal magnitude and independent of frequency and phase angle.
Peak to Peak Voltage
The RMS voltage of a sinusoidal waveform can be obtained by multiplying peak to peak voltage with 1/2√2. That is
Vrms= Vp-px 1 / 2√2
= Vp-px 0.353
Average Voltage
The RMS voltage of a periodic waveform or alternating waveform is given as,
Vrms= Vavg x π / 2√2=
Vavg *1.1107
Sinusoidal RMS Values
Sinusoidal RMS values the magnitudes of the voltage and current values. These values are equivalent to the DC values. Measuring instruments like ammeters and voltmeters are used to measure the RMS values of the AC signal.
The sinusoidal RMS values are calculated by using the following formulae,
Vrms = Vpeak* (1/√2)= Vpeak*0.7071
Vrms= Vp-px 1 / 2√2= Vp-p x 0.353
Vrms= Vavgx π / 2√2
=Vavg*1.1107
Thus, this is all about the RMS voltage (root mean square) – definition, theory, analytical method, graphical method, equation, and Values. The purpose of the RMS voltage is to find the magnitude of the voltage of the AC waveform, form factor, and crest factor to analyze the system performance. Here is a question for you, “What is the average value of a sinusoidal waveform?”