 Comparators are classified into various kinds, such as electronic, electrical, mechanical, optical, sigma, digital and pneumatic comparators, these are used in various applications. Comparators play an essential role in designing electrical and electronic projects. In electronic circuits, an op-amp is used with negative feedback and it can also be used as a comparator. The comparator is mainly designed without feedback for open loop configuration. These are widely used in A/D converters. When the i/p signal is sampled, then this signal is applied to multiple comparators to convert the digital form from analog.
Comparators are classified into various kinds, such as electronic, electrical, mechanical, optical, sigma, digital and pneumatic comparators, these are used in various applications. Comparators play an essential role in designing electrical and electronic projects. In electronic circuits, an op-amp is used with negative feedback and it can also be used as a comparator. The comparator is mainly designed without feedback for open loop configuration. These are widely used in A/D converters. When the i/p signal is sampled, then this signal is applied to multiple comparators to convert the digital form from analog.
The applications of comparators mainly involve in BLDC operating motors, zero crossing detectors, switching power regulators and peak detectors.This article gives an overview of what is a comparator and types of comparators.
What is a Comparator?
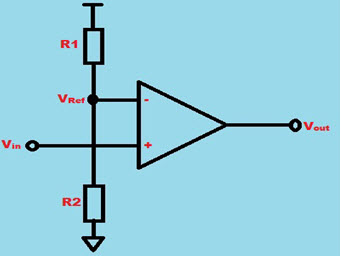
In general, a comparator is defined as, a device which includes two i/p terminals namely inverting and non inverting terminals.One input terminal is fed with reference i/p signal and the remaining i/p is fed with the actual values of the signal. The o/p signal can be generated based on the difference between two i/p signals either high or low. Here low and high signals are denoted by 0 and . The main purpose of the comparator is to compare two currents or voltages which are fed to the two i/p signals and generates binary digital o/p signal that specifies which is greater is called as a comparator.
 Comparator
Comparator
The two i/p terminals of the comparators are V+ and V- and the digital o/p is V0.
This o/p signal can be defined as
If V+ is greater than V- then V0 = 1and
If V+ is less than V- then V0 = 0,
Types of Comparators
Comparators are classified into different types such as
- Mechanical Comparator
- Mechanical-Optical Comparator
- Reed Type Comparator
- Electrical-Electronic Comparator
- Pneumatic Comparator
Mechanical Comparator
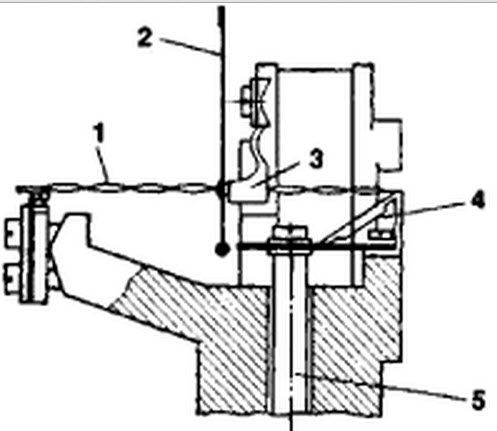
The term mechanical comparator is also called as “microcator”. In mechanical comparators, magnification is achieved by various mechanical devices and mechanical linkages. Mechanical comparator is a measuring instrument and the mechanism of this instrument is in the form of tape spring twisted, and that is positioned in the middle part. The middle part of the mechanical comparator rotates through a fixed angle upon tension which is shown in the figure. This comparator is used for linear measurements by using relative contact method. This comparator is designed in the year 1930 by the Johanson Company of Sweden.
 Mechanical Comparator
Mechanical Comparator
The above mechanical comparator comprises the following parts, they are Spring, Pointer, Pointer Attachment Fitting, Damping Lever and Measurement Spindle
The length, which is measured is shown by a pointer on a scale, here pointer is attached to the middle part of the spring. The attached pointer is proportional to the spring rotation angle. Mechanical comparator is fixed on a pedestal to make measurements. It is frequently adjusted to the necessary size of an end standard, that is arranged between the instrument’s tip & the plane of the pedestal table. The applications of the mechanical comparator mechanism involve in spring level indicators, small spring measuring heads, micators and spring optical measuring heads. Mechanical comparators are classified into four types such as
- Dial Gauge Comparator
- Johansson Mikrokator Comparator
- Reed Type Comparator
- Sigma Comparator.
Mechanical-Optical Comparator
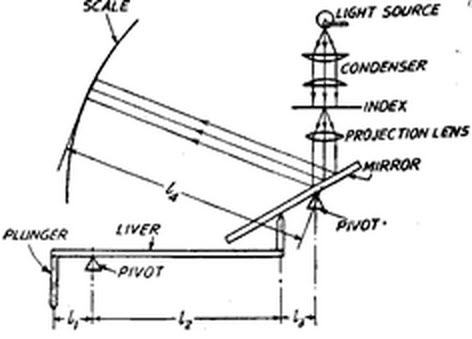
In mechanical-optical comparator, a small dislocation of the measuring plunger is first amplified by a mechanical system comprising of pivoted levers. Further, the mechanical movement which is amplified by an optical system connecting the outcrop an image. The general arrangement of mechanical system causes a reflector to angle near the image and an axis of an index estimated on a scale on the inner glass screen. Optical magnification offers a high degree of precision measuring.
 Mechanical-Optical Comparator
Mechanical-Optical Comparator
In the above system, mechanical amplification is multiplied by optical amplification. Because, if the mirror is sloped by an angle 60, then the image will be sloped by 2×66. Therefore, the total magnification of the system is 2 x (Z^i) (J4//3).
Thus, it is clear that optical comparators are proficient of giving a high degree of calculating accuracy owing to high magnification & the discount off moving members to a minimum. Further, these have a better wear resistance qualities and the main advantage of this comparator is that deliver of an illumined scale allows readings to be taken without favor to the conditions of room lighting. In this type of comparator, front reflection type mirror is used instead of normal back reflection type mirror. In normal back reflection mirror type, there are two reflected images such as front and back. Thus, the reflected image is not defined well, the two images. One image is bright and other one is blurred both are observed. When the front reflection type mirror is used, then it needs huge care in its use to avoid the damage to the shiny surfaces.
Reed Type Comparator
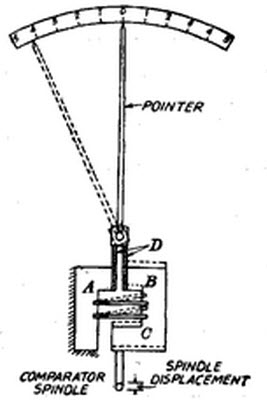
The Reed Type Comparator figure is shown below. This is a frictionless device for expanding small motions of the spindle. It comprises of a static block A, which is strictly attached to the gauge head case. The floating block B carries the gauging spindle & is connected horizontally to the static block by reeds C. A perpendicular reed is attached to every block with the higher ends combined together, as shown in the below figure. A linear motion of the spindle travels the free block perpendicularly causing the perpendicular reed to slide. This effort roots the target to swing through an arc over the scale related to the distance moved by the spindle. This type of comparators may have the compassions of the order of 0.25 micro/scale division.
 Reed Type Comparator
Reed Type Comparator
Electric Comparators
An electrical comparator consists of a base a stand, power unit, measuring unit, indication unit and amplification unit. In this comparator, the measuring contact movement is changed into an electrical signal and then this signal is recorded by a device that can be adjusted in terms of plunger movement. For this, an AC Wheatstone bridge circuit including a galvanometer is used.
This electric comparator comprises of a tough stylus, an iron armature that breaks against the W and spring and W1.If the armature is located between the coils W & W1, then the inductance of these coils is equal; the Wheatstone bridge is stable and forms the datum line.
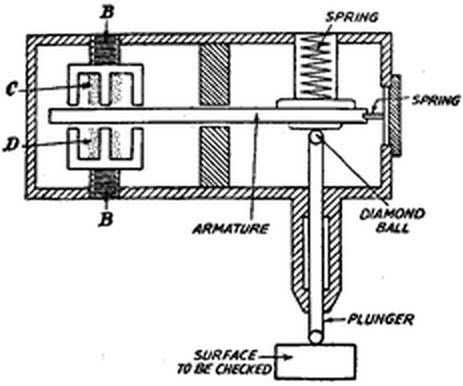 Electric Comparators
Electric Comparators
When the workpiece is located under the stylus for the measurement purpose due to the difference in datum. The armature, component size would either be raised up or down. It defeats the Wheatstone bridge balance that results the unbalanced current flow. This current is directly adjusted into difference in size of the component which is expanded by an amplifier specified by the galvanometer.These comparators have a precision of 0.001 mm. The main advantages of these comparators are no moving parts, sensitivity and accuracy over long periods.
Pneumatic Comparator
The working principle of pneumatic comparator is, when the air under constant pressure discharges by passing through two openings. If one of the hole is kept uniform, the pressure will change according to the size of the other. In the following diagram, the tube 1is connected to an air supply & via restriction jets2 to pipe 11 which dips into water in a deep vessel open to the atmosphere. Air flowing at tube 1 increases in pipe 11 and keeps a fixed head of water-H and extra of air outflows as bubbles. Air from pipe11 flows through control jet3 & finally outflows through the measuring jet at 6.
 Pneumatic Comparator
Pneumatic Comparator
The pressure in the tube b/n control jet 3 and calculating jet6 will depend on the orifice size at 6, which is controlled by the distance b/n the measuring table and face, and is replicated by the height of a liquid in the manometer pipe8. The scale 9 is also adjusted that a head difference h specifies changes in the gap d enlarged various hundred times. The main advantages of this comparator is, easy to operate, cheap, independent of the constant pressure, free from mechanical wear and magnification is high as 10,000 times.
Please refer to this link to know about Comparator MCQ
Thus, this is all about a comparator and the types of comparators which includes mechanical, optical, Reed type, electrical and pneumatic comparators. We hope that you have got a better concept of this article. Here is a question for you, what is the function of the comparator?
Photo Credits
- Mechanical Comparator by tfd